إدارة منتديات 
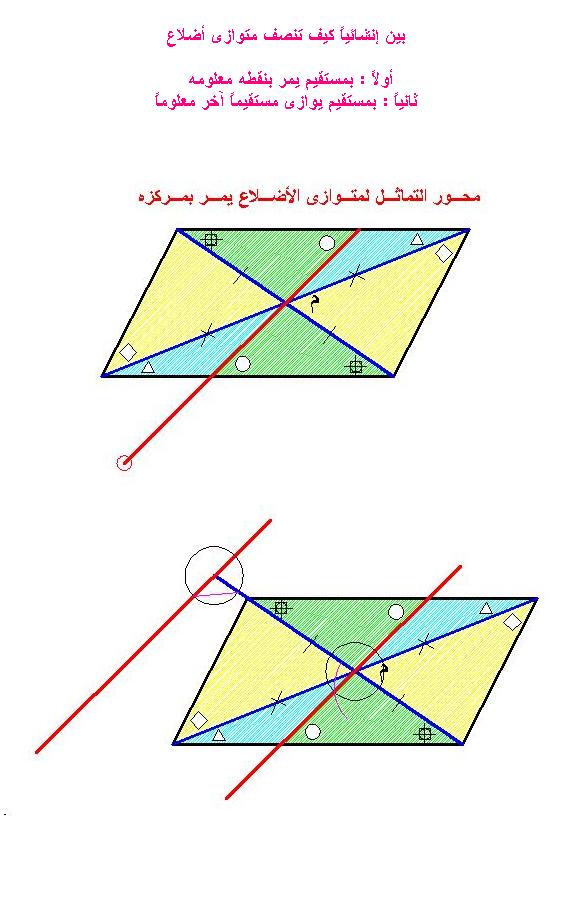
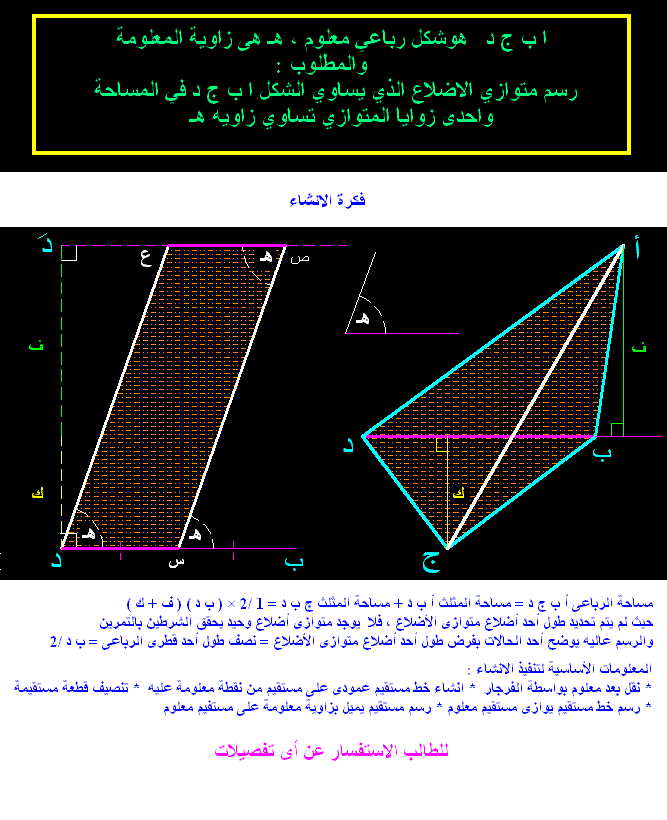
تحويل مستطيل الى مربع بنفس المساحة
رسم قطعة طولها يساوي الجذر التكعيبي للعدد 2 باستخدام مسطرة مدرجة وفرجار
العمل :
نرسم القطعة المستقيمة أ و = 1 ( وحدة طول )
نرسم من نقطة و شعاع عمودى على القطعة المستقيمة أ و
نرسم من نقطة و شعاع يميل على القطعة المستقيمة أ و بزاوية 60 درجة
بواسطة مسطرة مدرجة نرسم المستقيم أ ج يقطع الشعاع المائل فى نقطة ج ،
والشعاع العمودى فى نقطة ب ، بحيث القطعة المستقيمة ب ج = القطعة
المستقيمة أ و = 1 ( وحدة طول )
وذلك بتحريك المسطرة المدرجة المستندة على النقطة أ حتى يتحقق ذلك ( وهو أمر سهل )
نقيس القطعة المستقيمة أ ب = س
وهى تمثل الجذر التكعيبى للعدد 2
علما بأن المقدار المقاس تقريبى ويعتمد على مقياس الرسم
البرهان :
س/1 = (س + 1)/(1 + م)
ومنها : م = 1/س
ع/1 = جذرتربيعى(3) *م /(1 + م)
بالتعويض عن قيمة م بدلالة س : م = 1/س
ع = جذرتربيعى(3)/(س + 1)
ع^2 = 3/(س + 1)^2
من نظرية فيثاغورث : س^2 = ع^2 + (1)^2
بالتعويض عن قيمة ع^2 : ع^2 = 3/(س + 1)^2
س^2 = 3/(س + 1)^2 + 1
س^2 * (س + 1)^2 = 3 + (س + 1)^2
س^2 * ( س^2 + 2س + 1 ) = 3 + س^2 + 2س + 1
س^4 + 2 س^3 + س^2 = س^2 + 2 س + 4
س^4 + 2 س^3 = 2 س + 4
س^3 * (س + 2) = 2 * ( س + 2)
س^3 = 2
س = الجذر التكعيبى للعدد (2)
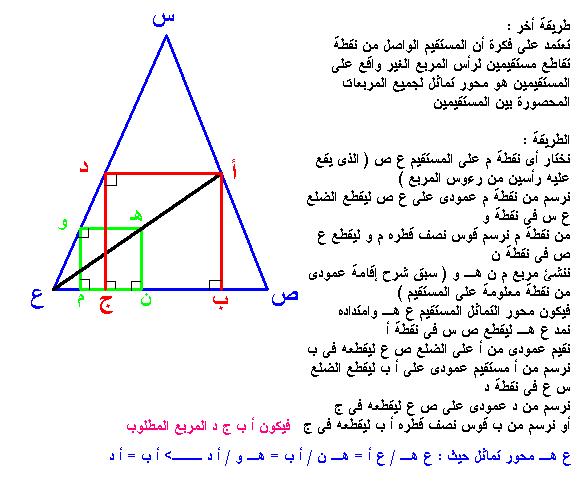
إنشاء مربع داخل مثلث معلوم
تحويل شكل المربع الى مستطيل مساوى له فى المساحة
وسأعرض بعض الطرق لتحويل شكل المربع المعلوم الى شكل المستطيل المساوى له فى المساحة
وهى تصلح أيضا لتحويل شكل المستطيل المعلوم الى شكل المربع المساوى له فى المساحة
تنويه :
من الصعوبة تحويل الشكل المعلوم ( مربع أو مستطيل ) الى الآخر المحدد
أبعاده سلفا ، والغالب أن تكون أبعاد الشكل المحوّل إليه عشوائية إلا فى
حدود أو نسب معينة
الطريقة الأولى
الطريقة الثانية
الطريقة الثالثة
وتعطى أبعاد محددة للمستطيل جذر5*ل/2 × 2 ل/جذر5
طرق أخرى
